Poker in 2018 is as competitive as it has ever been. Long gone are the days of being able to print money playing a basic ABC strategy.

• Poker Texas Holdem Kombinationen, blauwe slot 25 goutum, mgm casino near washington dc, martijn slot hengelo.
• A lot of online poker rooms offer 'freerolls' which are free-to-enter poker tournaments with real prizes. They generally pay out 10-15% of the field in cash, tournament tickets and other goodies. The Poker.com freeroll tracker page lists upcoming freerolls from the.
• The minimum qualifying deposit Kombinationen Poker is €10 or other currency equivalent. Players need to wager the bonus amount 25 times before any withdrawals can be made. Players have 30 days to complete the wagering requirements. Games contribute different to wagering requirements. 18+, New Players Only. Wagering Requirements.

Today your average winning poker player has many tricks in their bags and tools in their arsenals. Imagine a soldier going into the heat of battle. Without his weapons, he is practically useless, and chances of survival are extremely low.

If you sit down at a poker table without any preparation or general understanding of poker fundamentals, the sharks are going to eat you alive. Sure you may get lucky once in a blue moon, but over the long term, things won’t end well.

With the evolution of poker strategy, you now have many tools at your disposal. Whether it be online poker training sites, free YouTube content, poker coaching, or poker vlogs, there’s no excuse to be a fish in today's game.

Alle Rechte vorbehalten.

Some of the essential fundamentals you need to be utilizing that every poker player should have in their bag of tricks whether you are a Tournament or Cash Game Player are concepts such as hand combinations (Also known as hand combinatorics or hand combos).

Hand Combinations and Hand Reading

If you were to analyze a large sample of successful poker players you would notice that they all have one skill set in common: Hand Reading

What does hand reading have to do with hand combinations you might ask?

Well, poker is a game of deduction and to be a good hand reader, you need to be good at correctly ranging your opponents.

Once you have assigned them a range, you will then need to start narrowing that range down. Combinatorics is one of the ways we do this.

So what is combinatorics? It may sound like rocket science and it is definitely a bit more complex than some other poker concepts, but once you get the hang of combinatorics it will take your game to the next level.

Combinatorics is essentially understanding how many combos each of your opponent's potential holdings are and deducing their potential holdings utilizing concepts such as removal and blockers.

There are 52 cards in a deck, 13 of each suit, and 4 of each rank with 1326 poker hands in total. To simplify things just focus on memorizing all of the potential combos to start:

• 16 possible hand combinations of every unpaired hand
• 12 combinations of every unpaired offsuit hand
• 4 combinations of each suited hand
• 6 possible combinations of pocket pairs

Here is a short video example of using combinatorics to count the number of ways a non-paired hand AK can be arranged (i.e. how many combos there are):

So now that we have this memorized, let's look at a hand example and how we can apply combinatorics in game.

We hold A♣Q♣ in the SB and 3bet the BTN’s open to 10bb with 100bb stacks. He flats and we go heads up to a flop of

A♠ 5♦ 4♦

We check and our opponent checks back with 21bb in the middle

Turn is the 4♥

We bet 10bb and our opponent calls for a total pot of 41bb

The river brings the 9♠

So the final board reads

A♠ 5♦ 4♦ 4♥ 9♠

We bet 21bb and our opponent jams all in leaving us with 59bb to call into a pot of 162bb resulting in needing at least 36% pot equity to win.

Our opponent is representing a polarized range here. He is either nutted or representing missed draws so we find ourself in a tough spot. This is where utilizing combinatorics to deduce his value hands vs bluffs come into play. Now we need to narrow down his range given our line and his line. Let's take a look at how we do this...

Free MTT Poker Training:

The Underused MTT Skills Essential For Success

• 5 Day Email MTT Poker Training Course By Poker Pro Kelvin 'Acesup' Beattie
• 3 Key Skills That Will Take Your MTT Poker Game To A New Level
• 1.5 Hours Of Professional Poker Training

Blockers and Card Removal Effects

First, let's take a look at the hands we BLOCK and DON’T BLOCK

Since we hold an Ace in our hand and there is an Ace on the board, that only leaves 2 Ace’s left in the deck. So there is exactly 1 combo of AA.

We BLOCK most of the Aces he can be holding, so we can REMOVE some Aces from his range.

We do not BLOCK the A♦ as we hold A♣Q♣, and the A on the board is a spade, so it is still possible for him to have some A♦x♦ hands.

We checked flop to add strength to our check call range (although a bet with a plan to triple barrel is equally valid in this situation SB vs BTN) and because of this our opponent may not put us on an A here.

If he is a thinking player his jam can exploit our thin value bet on the river turning his missed straight/flush draws into a bluff to get us to fold our big pocket pairs and even make it a tough call with our perceived weak holdings.

The problem in giving him significant credit for this part of his bluffing range is the question of would he really shove here with good SDV (Showdown Value)?

These are the types of questions we must ask ourselves to further deduce his range along with applying the combinatoric information we now have.

Now, let's look at all the nutted Ax hands our opponent can have.

If he has a nutted hand like A4 or A5, and we assume he is only calling 3bets with Axs type hands, the only suited combo of those hands he can have are exactly A♥5♥. He can’t have A♦5♦ or A♦4♦ because the 4 and the 5 are both diamonds on the board blocks these hands.

Lets take a look at all of this value hands:

There is only 1 combo of 44 left in the deck, 2 combos of A9s, 3 Combos of 55, 3 Combos of 99, 2 Combos of 45s - some of these hands may also be bet on the flop when facing a check.

So to recap we have:

1 Combo A5s, 2 Combos of A9s, 3 Combos of 55 (With one 5 on board, the number of combinations of 55 are cut in half from 6 combos to 3 combos), 1 Combo of 44, 2 Combos of 45s, 3 Combos of 99

Total: 12 Value Combos

Now we need to look at our opponent's potential bluffs

Based on the villain's image, this is the range of bluffs we assigned him:

K♦Q♦(1 Combo), J♦T♦ (1 Combo), T♦9♦ (1 Combo), 67s (4 Combos)

He may also turn some other random hands with little showdown value into bluffs such as A♦2♦/A♦3♦

Total: 9 Bluff Combos

9(Bluff Combos) + 12(Value Combos) = 22

9/21 = 42% of the time our opponent will be bluffing (assuming he always bets this entire range)

11/21 = 58% of the time our opponent will be value raising

Now, this is the range we assigned him in game based on the action and what we perceived our opponents range to be.

We are not always correct in applying the exact range of his potential holdings, but so long as you are in the ballpark of that range you can still make quite a few deductions to put yourself in the position to make the correct final decision.

According to the range we assigned him, he has 11 Value Combos and 9 Bluff Combos which gives us equity of 42%. This would result in a positive expected value call as we only need 36% pot odds to call.

However, unless you are playing against very tough opponents you will not see someone bluffing all 9 combos we have assigned - most likely they will bluff in the range of 4-6 combos on average which gives equity in the range of 20-30% equity. This is not enough to call.

We ultimately made our decision based on the fact that we felt our opponent was much less likely to jam with his bluffs in this spot. Given that it was already a close decision to begin with, we managed to find what ended up being the correct fold.

Now this all may seem a bit overwhelming, but if you just start taking an extra minute on your big decisions you’d be surprised how quickly you can actually process all this information on this spot.

A good starting point is to simply memorize all of the possible hand combinations listed above near the beginning of the article.

Get access to our 30-minute lesson on Combinatorics and PokerStove by clicking on one of the buttons below:

Conclusion On Combinatorics

Eventually accounting for your opponent's combos in a hand will become second nature. To get to the point that , a lot of the work needs to be done off the table and in the lab. As you spend more time studying it and reviewing hand histories like the one above, you will find yourself intuitively and almost subconsciously using combinatorics in your decision making tree.

But the work will be worth the effort, as being able to count combos on the fly will add a new dimension to your game, allow you to make more educated decisions, become a tougher opponent to play against and move away from playing ABC poker.

Want more content like the ones in this blog post on poker combinatorics? Check out our Road to Success Course where we have almost 100 videos like this to help take your game to the next level. You can also get the first module of the Road To Success Course for Free - for more details see the free poker training videos page by TopPokerValue.com.

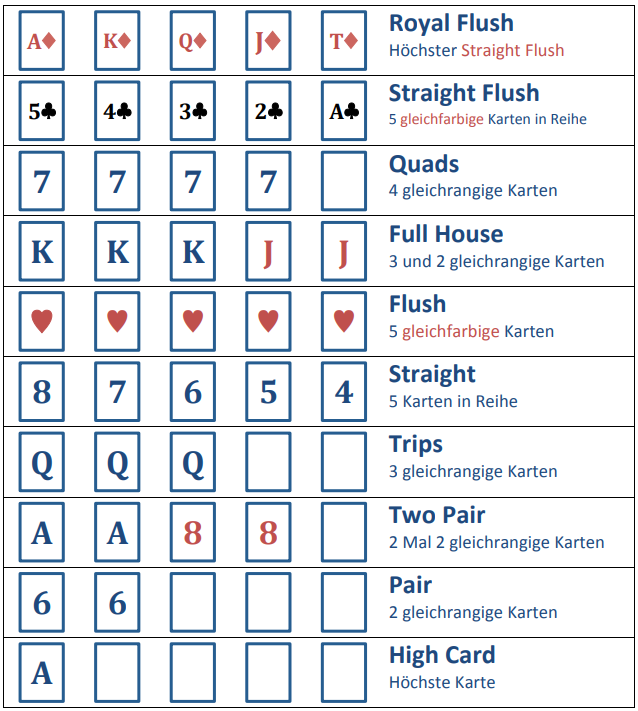
Poker Combinations Rank

For a great training video on poker combinatorics, check out this poker combos video.

'Combinatorics' is a big word for something that isn’t all that difficult to understand. In this article, I will go through the basics of working out hand combinations or 'combos' in poker and give a few examples to help show you why it is useful.

Oh, and as you’ve probably noticed, 'combinatorics', 'hand combinations' and 'combos' refer to the same thing in poker. Don’t get confused if I use them interchangeably, which I probably will.

What is poker combinatorics?

Poker combinatorics involves working out how many different combinations of a hand exists in a certain situation.

For example:

• How many ways can you be dealt AK?
• How many ways can you be dealt 66?
• How combinations of T9 are there on a flop of T32?
• How many straight draw combinations are there on a flop of AT7?

Using combinatorics, you will be able to quickly work these numbers out and use them to help you make better decisions based on the probability of certain hands showing up.

Poker starting hand combinations basics.

• Any two (e.g. AK or T5) = 16 combinations
• Pairs (e.g. AA or TT) = 6 combinations

If you were take a hand like AK and write down all the possible ways you could be dealt this hand from a deck of cards (e.g. A K, A K, A K etc.), you would find that there are 16 possible combinations.

See all 16 AK hand combinations:

Similarly, if you wrote down all the possible combinations of a pocket pair like JJ (e.g. JJ, JJ, JJ etc.), you would find that there are just 6 possible combinations.

See all 6 JJ pocket pair hand combinations:

So as you can see from these basic starting hand combinations in poker, you’re almost 3 times as likely to be dealt a non-paired hand like AK than a paired hand. That’s pretty interesting in itself, but you can do a lot more than this…

Note: two extra starting hand combinations.

As mentioned above, there are 16 combinations of any two non-paired cards. Therefore, this includes the suited and non-suited combinations.

Here are 2 extra stats that give you the total combinations of any two suited and any two unsuited cards specifically.

• Any two (e.g. AK or 67 suited or unsuited) = 16 combinations
• Any two suited (AKs) = 4 combinations
• Any two unsuited (AKo) = 12 combinations
• Pairs (e.g. AA or TT) = 6 combinations

You won’t use these extra starting hand combinations nearly as much as the first two, but I thought I would include them here for your interest anyway.

It’s easy to work out how there are only 4 suited combinations of any two cards, as there are only 4 suits in the deck. If you then take these 4 suited hands away from the total of 16 'any two' hand combinations (which include both the suited and unsuited hands), you are left with the 12 unsuited hand combinations. Easy.

Fact: There are 1,326 combinations of starting hands in Texas Hold’em in total.

Working out hand combinations using 'known' cards.

Let’s say we hold KQ on a flop of KT4 (suits do not matter). How many possible combinations of AK and TT are out there that our opponent could hold?

Unpaired hands (e.g. AK).

How to work out the total number of hand combinations for an unpaired hand like AK, JT, or Q3.

Method: Multiply the numbers of available cards for each of the two cards.
Word equation: (1st card available cards) x (2nd card available cards) = total combinations

Example.

If we hold KQ on a KT4 flop, how many possible combinations of AK are there?

There are 4 Aces and 2 Kings (4 minus the 1 on the flop and minus the 1 in our hand) available in the deck.

C = 8, so there are 8 possible combinations of AK if we hold KQ on a flop of KT4.

Paired hands (e.g. TT).

How to work out the total number of hand combinations for an paired hand like AA, JJ, or 44.

Method: Multiply the number of available cards by the number of available cards minus 1, then divide by two.
Word equation: [(available cards) x (available cards - 1)] / 2 = total combinations

Example.

How many combinations of TT are there on a KT4 flop?

Well, on a flop of KT4 here are 3 Tens left in the deck, so…

C = 3, which means there are 3 possible combinations of TT.

Thoughts on working out hand combinations.

Working out the number of possible combinations of unpaired hands is easy enough; just multiply the two numbers of available cards.

Working out the combinations for paired hands looks awkward at first, but it’s not that tricky when you actually try it out. Just find the number of available cards, take 1 away from that number, multiply those two numbers together then half it.

Alle Poker Kombinationen

Note: You’ll also notice that this method works for working out the preflop starting hand combinations mentioned earlier on. For example, if you’re working out the number of AK combinations as a starting hand, there are 4 Aces and 4 Kings available, so 4 x 4 = 16 AK combinations.

Why is combinatorics useful?

Because by working out hand combinations, you can find out more useful information about a player’s range.

For example, let’s say that an opponents 3betting range is roughly 2%. This means that they are only ever 3betting AA, KK and AK. That’s a very tight range indeed.

Now, just looking at this range of hands you might think that whenever this player 3bets, they are more likely to have a big pocket pair. After all, both AA and KK are in his range, compared to the single unpaired hand of AK. So without considering combinatorics for this 2% range, you might think that the probability break-up of each hand looks like this:

• AA = 33%
• KK = 33%
• AK = 33%

…with the two big pairs making up the majority of this 2% 3betting range (roughly 66% in total).

However, let’s look at these hands by comparing the total combinations for each hand:

• AA = 6 combinations (21.5%)
• KK = 6 combinations (21.5%)
• AK = 16 combinations (57%)

So out of 28 possible combinations made up from AA, KK and AK, 16 of them come from AK. This means that when our opponent 3bets, the majority of the time he is holding AK and not a big pocket pair.

Now obviously if you’re holding a hand like 75o this is hardly comforting. However, the point is that it’s useful to realise that the probabilities of certain types of hands in a range will vary. Just because a player either has AA or AK, it doesn’t mean that they’re both equally probable holdings - they will actually be holding AK more often than not.

Analogy: If a fruit bowl contains 100 oranges, 1 apple, 1 pear and 1 grape, there is a decent range of fruit (the 'hands'). However, the the fruits are heavily weighted toward oranges, so there is a greater chance of randomly selecting an orange from the bowl than any of the 3 other possible fruits ('AK' in the example above).

This same method applies when you’re trying to work out the probabilities of a range of possible made hands on the flop by looking at the number of hand combinations. For example, if your opponent could have either a straight draw or a set, which of the two is more likely?

Poker combinatorics example hand.

You have 66 on a board of A J 6 8 2. The pot is $12 and you bet $10. Your opponent moves all in for $60, which means you have to call $50 to win a pot of $82.

You are confident that your opponent either has a set or two pair with an Ace (i.e. AJ, A8, A6 or A2). Don’t worry about how you know this or why you’re in this situation, you just are.

According to pot odds, you need to have at least a 38% chance of having the best hand to call. You can now use combinatorics / hand combinations here to help you decide whether or not to call.

Poker combinatorics example hand solution.

First of all, let’s split our opponent’s hands in to hands you beat and hands you don’t beat, working out the number of hand combinations for each.

Poker Combinations Printable

Adding them all up…

Seeing as you have the best hand 79% of the time (or 79% 'equity') and the pot odds indicate that you only need to have the best hand 38% of the time, it makes it +EV to call.

So whereas you might have initially thought that the number of hands we beat compared to the number of hands we didn’t beat was close to 50/50 (making it likely -EV to call), after looking at the hand combinations we can see that it is actually much closer to 80/20, making calling a profitable play.

Being able to assign a range to your opponent is good, but understanding the different likelihoods of the hands within that range is better.

Poker combinatorics conclusion.

Working out hand combinations in poker is simple:

• Unpaired hands: Multiply the number of available cards. (e.g. AK on an AT2 flop = [3 x 4] = 12 AK combinations).
• Paired hands: Find the number of available cards. Take 1 away from that number, multiply those two numbers together and divide by 2. (e.g. TT on a AT2 flop = [3 x 2] / 2 = 3 TT combinations).

Poker Kombinationen Deutsch

By working out hand combinations you can gain a much better understanding about opponent’s hand ranges. If you only ever deal in ranges and ignore hand combinations, you are missing out on useful information.

It’s unrealistic to think that you’re going to work out all these hand combinations on the fly whilst you’re sat at the table. However, a lot of value comes from simply familiarising yourself with the varying probabilities of different types of hands for future reference.

For example, after a while you’ll start to realise that straight draws are a lot more common than you think, and that flush draws are far less common than you think. Insights like these will help you when you’re faced with similar decisions in the future.

The next time you’re doing some post session analysis, spend some time thinking about combinatorics and noting down what you find.

Poker combinatorics further reading.

Hand combinations in poker all stem from statistics. So if you’re interested in finding out more about the math side of things, here are a few links that I found helpful:

• Combinations video - Youtube (all the stuff on this channel is awesome)

If you’re more interested in finding out more about combinations in poker only, here are a few interesting reads:

Go back to the awesome Texas Hold'em Strategy.

Poker Kombinationen Reihenfolge

Comments